Area Of Circle

Circle:

A circle is easy to make: Draw a curve that is "radius" away from a central point.

And so: All points are the same distance from the center.

You Can Draw It Yourself

Put a pin in a board, put a loop of string around it, and insert a pencil into the loop. Keep the string stretched and draw the circle!

Radius, Diameter and Circumference

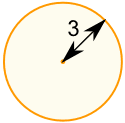
The Radius is the distance from the center outwards.

The Diameter goes straight across the circle, through the center.

The Circumference is the distance once around the circle.

And here is the really cool thing:

When we divide the circumference by the diameter we get 3.141592654...
which is the number π (Pi)

So when the diameter is 1, the circumference is 3.141592654...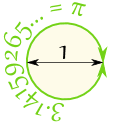

We can say:

Circumference = π × Diameter

Example: You walk around a circle which has a diameter of 100m, how far have you walked?

Distance walked = Circumference = π × 100m

= 314m (to the nearest m)

Also note that the Diameter is twice the Radius:

Diameter = 2 × Radius

And so this is also true:

Circumference = 2 × π × Radius

In Summary:

× 2	× π

Radius

Diameter

Circumference

Remembering

The length of the words may help you remember:

• Radius is the shortest word and shortest measure
• Diameter is longer
• Circumference is the longest

Definition

The circle is a plane shape (two dimensional), so:

Circle: the set of all points on a plane that are a fixed distance from a center.

Area

The area of a circle is π times the radius squared, which is written:

A = π r²

Where

• A is the Area
• r is the radius

To help you remember think "Pie Are Squared" (even though pies are usually round):

Example: What is the area of a circle with radius of 1.2 m ?

Area= πr²

 = π × 1.2²

 = 3.14159... × (1.2 × 1.2)

 = 4.52 (to 2 decimals)

Or, using the Diameter:

A = (π/4) × D²

Area Compared to a Square

A circle has about 80% of the area of a similar-width square.
The actual value is (π/4) = 0.785398... = 78.5398...%

Names

Because people have studied circles for thousands of years special names have come about.

Nobody wants to say "that line that starts at one side of the circle, goes through the center and ends on the other side" when they can just say "Diameter".

So here are the most common special names:

Lines

A line that "just touches" the circle as it passes by is called a Tangent.

A line that cuts the circle at two points is called a Secant.

A line segment that goes from one point to another on the circle's circumference is called a Chord.

If it passes through the center it is called a Diameter.

And a part of the circumference is called an Arc.

Slices

There are two main "slices" of a circle.
The "pizza" slice is called a Sector.
And the slice made by a chord is called a Segment.

Common Sectors

The Quadrant and Semicircle are two special types of Sector:

Quarter of a circle is called a Quadrant.

Half a circle is called a Semicircle.

Inside and Outside

A circle has an inside and an outside (of course!). But it also has an "on", because we could be right on the circle.

Example: "A" is outside the circle, "B" is inside the circle and "C" is on the circle.

Ellipse

A circle is a "special case" of an ellipse.

Area of a Circle:

Calculation:

The radius, diameter, circumference or area of a Circle to find the other three. How the calculations are done:

How to Calculate the Area

The area of a circle is:

π (Pi) times the Radius squared:A = π r²

or, when you know the Diameter:A = (π/4) × D²

or, when you know the Circumference:A = C² / 4π

Example: What is the area of a circle with radius of 3 m ?

Radius = r = 3

Area= π r²

 = π × 3²

 = 3.14159... × (3 × 3)

 = 28.27 m² (to 2 decimal places)

How to Remember?

To help you remember think "Pie Are Squared"
(even though pies are usually round)

Comparing a Circle to a Square

It is interesting to compare the area of a circle to a square:

A circle has about 80% of the area of a similar-width square.
The actual value is (π/4) = 0.785398... = 78.5398...%

Why? Because the Square's Area is w²
and the Circle's Area is (π/4) × w²

Example: Compare a square to a circle of width 3 m

Square's Area = w² = 3² = 9 m²
Estimate of Circle's Area = 80% of Square's Area = 80% of 9 = 7.2 m²
Circle's True Area = (π/4) × D² = (π/4) × 3² = 7.07 m² (to 2 decimals)

The estimate of 7.2 m² is not far off 7.07 m²

A "Real World" Example

Example: Max is building a house. The first step is to drill holes and fill them with concrete.

The holes are 0.4 m wide and 1 m deep, how much concrete should Max order for each hole?

The holes are circular (in cross section) because they are drilled out using an auger.
The diameter is 0.4m, so the Area is:

A = (π/4) × D²

A = (3.14159.../4) × 0.4²

A = 0.7854... × 0.16

A = 0.126 m² (to 3 decimals)

And the holes are 1 m deep, so:

Volume = 0.126 m² × 1 m = 0.126 m³

So Max should order 0.126 cubic meters of concrete to fill each hole.

Note: Max could have estimated the area by:

• 1. Calculating a square hole: 0.4 × 0.4 = 0.16 m²
• 2. Taking 80% of that (estimates a circle): 80% × 0.16 m² = 0.128 m²
• 3. And the volume of a 1 m deep hole is: 0.128 m³